Preguntas sobre el juego de moda

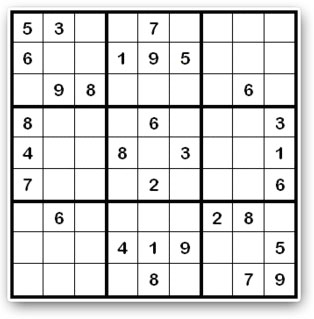Llevo casi todo el verano viciado de los sudokus. Para quien no lo sepa, se trata de un pasatiempo consistente en una cuadrícula de 9x9 casillas, subdividida en 9 cuadrados de 3x3. En alguna de las cuadrículas hay números entre el 1 y el 9 inclusive, y el objetivo del juego es rellenar todo el cuadrado, sabiendo que los números están sujetos a las siguientes condiciones:

a) En cada fila están todos los números del 1 al 9.
b) En cada columna también.
c) En cada cuadrado 3x3 también.

"Sudoku", de hecho, significa "número solo"; en http://www2.rincondelvago.com/servicios/sudoku/historia_del_susoku.html podéis encontrar una breve e interesante historia del pasatiempo.

Sin embargo, el motivo de este post no es hablar de mis maravillosas experiencias veraniegas, sino plantear algunas preguntas matemáticas, probablemente ya resueltas por cerebros de Ciencias de la Computación, que surgieron en una larga conversación que tuve con dos amigos hace unos días, mientras recorríamos Badajoz del derecho y del revés, y que no parecían tener respuesta sencilla. Asumimos que un sudoku debe tener solución única.

a) ¿Cuál es el la mínima cantidad de cifras de un sudoku? (Obsérvese que de forma trivial el cuadrado en blanco o el cuadrado con una cifra, por ejemplo, NO son sudokus)

b) ¿Cuál es el máximo número de cifras compatibles en un cuadrado 9x9 sin que sea sudoku?

c) Dada una cierta solución de un sudoku, ¿cuántos sudokus tienen esa misma solución? ¿Ese número es independiente de la solución?

d) ¿Cuántos sudokus hay? O lo que es más interesante: ¿cuántos sudokus hay salvo permutaciones del 1 al 9?

e) ¿Hay algún algoritmo SENCILLO que permita decidir si una configuración es sudoku o no? Por supuesto, la resolución habitual del sudoku es una prueba de que ocurre lo primero, pero la negación parece más difícil.

En fin, como podéis suponer, más que en las respuestas en sí estoy interesado en los razonamientos que lleven a ellas. Y si os coméis un poco la cabeza, nada mejor para desconectar que un buen sudoku, a ser posible con buena música de fondo ;-)

4 comentarios

[X. - 08 de octubre de 2005 - 15:12]

Y la poesía en el sudoku???? y la armonía literaria?? a ver, a ver, contestad a eso...
Me encanta leerte.
Me encantan los sudokus.
Echo de menos nuestras charlas y te advierto que he vuelto a pillar todo Tolkien...
Un gran abrazo

[Palimp - 12 de septiembre de 2005 - 10:17]

Realmente no, pero he visto por ahí que la solución a algunas de tus preguntas pasan por algoritmos de fuerza bruta (como por ejemplo el d)
La excursión, cuando quieras :)
Abrazos

[Cluje - 12 de septiembre de 2005 - 02:17]

Sí, sí que lo vi, Palimp, pero ¿el algoritmo da la solución a alguna de las preguntas que formulo en el post?

Por cierto, te emplazo a una excursión al Mercat de Sant Antoni antes de que acabe el mes.

[Palimp - 11 de septiembre de 2005 - 15:00]

Supongo que no habrás visto el 'resolvedor de sudokus':

www.liblit.com/sudoku

Bienvenido de vuelta.